文章信息：Minjin Lee, Hugo Barbosa, Hyejin Youn, Petter Holme, & Gourab Ghoshal. (2017). Morphology of travel routes and the organization of cities. Nature Communications: 8(1), 2229.https://doi.org/10.1038/s41467-017-02374-7

阅读笔记：黄丽云

阅读时间：2019年3月30日

选题视角：

城市街道网络是人口和资源流动的一个空间足迹活动，现有的研究大部分是针对道路结构本身的，对结构相互之间的影响、以及道路与城市动态关系的研究较少；并且，关于道路选择的偏好大部分是基于经验学的，路径的形态特征研究仍然较少。

路径的形态特征跟土地利用以及城市的动态因素关联性大，本次研究就选用了最短路径（受设计的局限和城市地形影响，简单的道路地理结构的函数）和最快路径（受交通和动态路线抽样的影响--不同的运输效率和拥挤模式引起的交通速度变化)。本研究的重大突破是确定了城市功能和街道布局之间的关系，以平衡快速城市化中心聚集或离散的趋势。

我们研究了92个城市中，分析47 2040条时空优化路线的形状。发现它们共有形态表现出的吸引力或排斥力，受拥挤、可达性和出行需求影响。为了捕捉这一点，我们开发了一个简单的几何度量，Inness描述最短路径和最快路径的相关函数，映射了这种聚集或离散的力场。

研究方法：

1.Sampling routing pairs.抽样路径的选择

（1）92个城市的城市中心和OD对选择：

通过引用latlong.net（获取经纬度的网站）的坐标来定义一个城市中心，并根据相对于中心和OD对的选择对旅行路线进行抽样。在球面坐标下(距中心r的距离，相对于中心θ的角度分离)。避免任何样本偏差，并系统地研究路由形态对距离城市中心的距离，我们只考虑固定半径r上的OD对。此外，在每个r中，我们以10°为间隔划分圆的圆周，共36点(为了避免噪声的影响，选择最小的角度间隔)。然后我们改变半径超过范围2，5，10，20，最后是30公里(大致对应于城市边界)，并通过将给定半径r上的36个点连接起来，计算出所有OD对。

最后，我们查询OpenStreetMapAPI中连接每对的建议旅行路线。用两个指标来描述道路功能特征（例如道路容量）和他们的等级组织：最短的，和最快的那一种。根据道路流量(即速度限制、车道数目等)计算的长度和行驶时间。图中展示了我们分割城市的方法的视觉表现。

2.Calculation of inness.指标的计算

Inness I是用鞋带公式求出路线上多边形数的面积之和计算I。

这里n是多边形的顶点数，m是路线上的多边形总数，(xi，j，yi，j)对应于多边形i的j‘th顶点的坐标，sgn(I)我们通过的内外点公约。

3.Data availability数据的可读性

评估结论所需的所有数据载于文件或补充材料。与本论文有关的其他数据可向作者索取，也可查阅。在https://github.com/mlee 96/Inness研究

其他及兴趣点：

大运河沿线城市，在不同的层面上都形成了区域尺度的重心；在历史上是否也有这样的相关要素可以通过一个复核的指标来模拟、衡量。

讨论：

从全球-中尺度研究，更能发掘街道-基础设施-城市社会经济之间的关系。

Inness模式表明，在城市中心街道密度较高、密度逐渐较低的城市中，大多数城市都存在核心-边缘结构。

结论和“中心位置理论”经典假设的若干要素相契合；并且和“多中心相互作用”理论的探讨，以及讨论了城市发展和土地利用的研究缺乏系统数据，而不成立。

总之，作为一个简单的度量标准，Inness对城市的几何、基础设施和社会经济信息进行了强有力编码，较为全面的展示城市的形象。

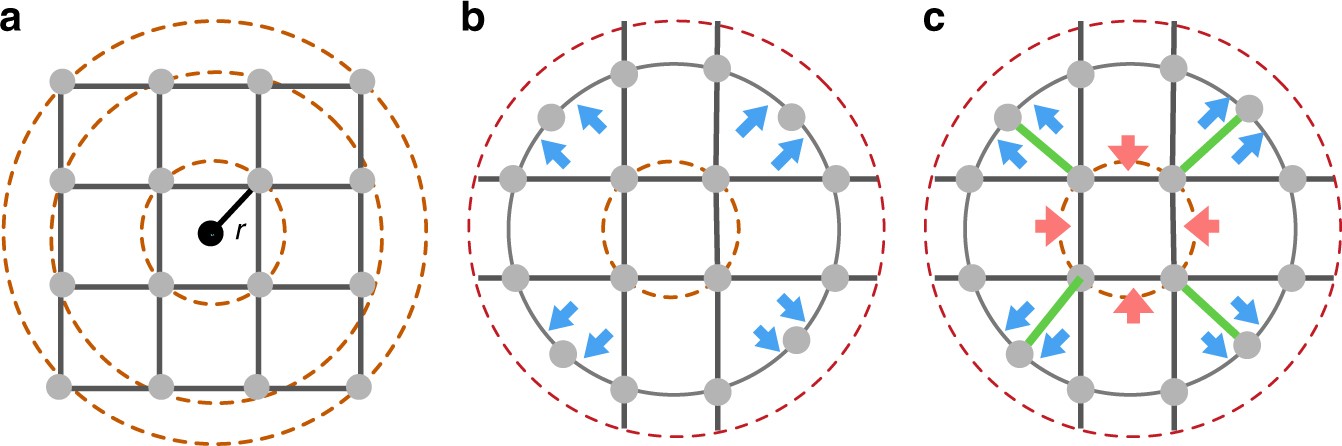
图 在城市形态中发现的偏置力

三种示意图的城市街道布局具有相似的拓扑结构，但不同的几何布局导致不同的动态。a网格结构，在相同半径的点之间的最短路径没有方向偏差。b当我们通过重新定位内等距环线上的四个外点来打破网格对称时，相对于原点（蓝色标记）的排斥力出现。位于这个环上的路径现在有了穿过外围并避开中心的最短路径。c通过增加与中心的连通性（标记为四条绿线）进一步扰乱拓扑，现在导致通过中心的最短路径，就好像存在吸引力（用红色标记）

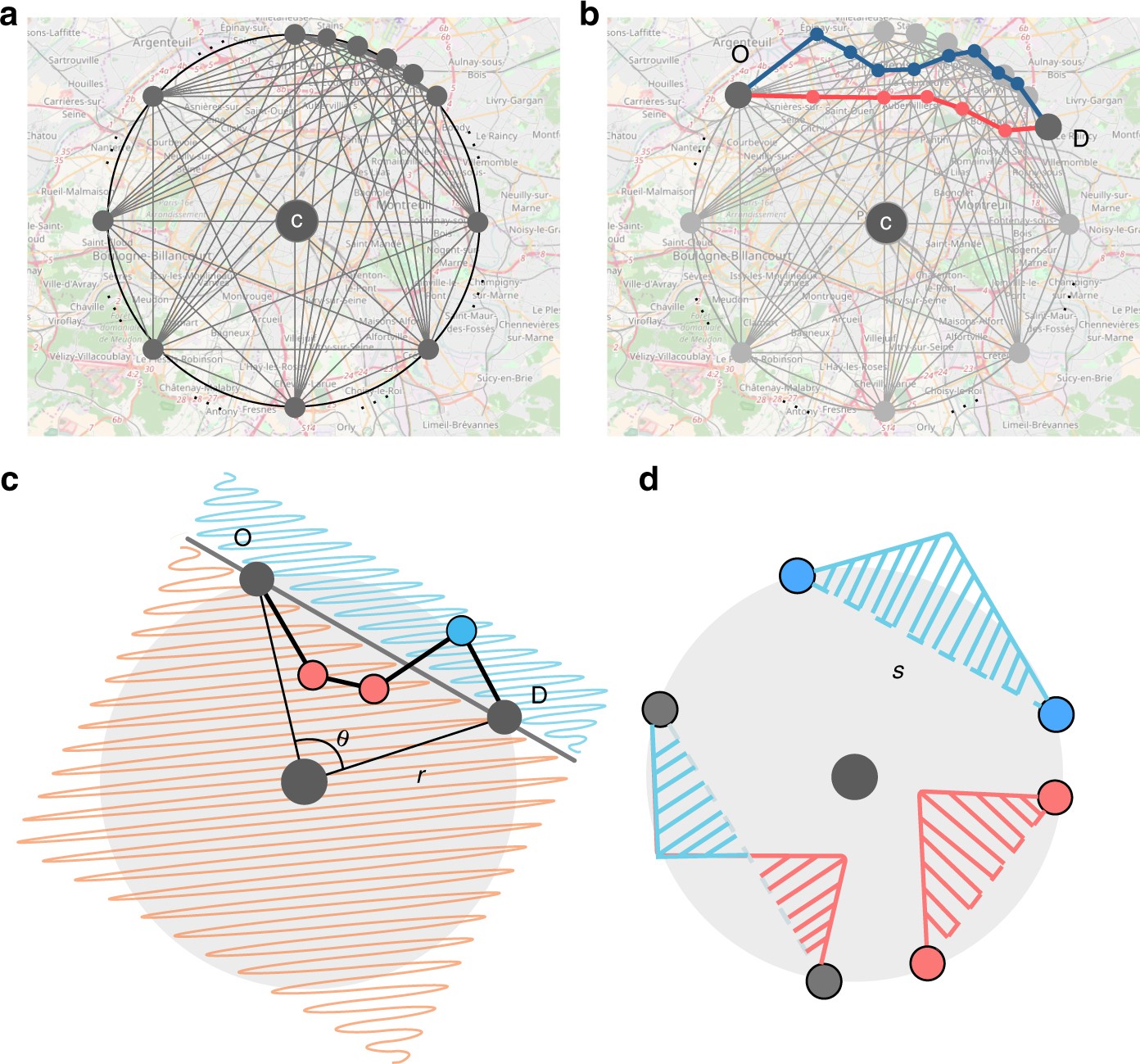
图 数据抽样和定义我36起源目的地（OD）对（间隔10°）分配沿圆周的距离2,5,10,15、20和30公里从城市中心C. b每个OD对，我们查询开源地图API和收集最短的路线（红色）和最快的路线（蓝色）（这里所示代表OD对在巴黎）。c一个典型的OD对，其连接的直线代表测地线距离s；r是距离中心的径向距离，θ是相对于中心的角距离。我们将内内性(I)定义为内部行程区域（红色内点和直线划定的多边形）和外部行程区域（蓝色外点和直线划定的多边形）之间的差值。d多个OD对之间的三种可能的路由配置。一个有一个单独的外部旅行区域（蓝色），一个有一个单独的内部旅行区域（红色），还有一个两者都有某种组合

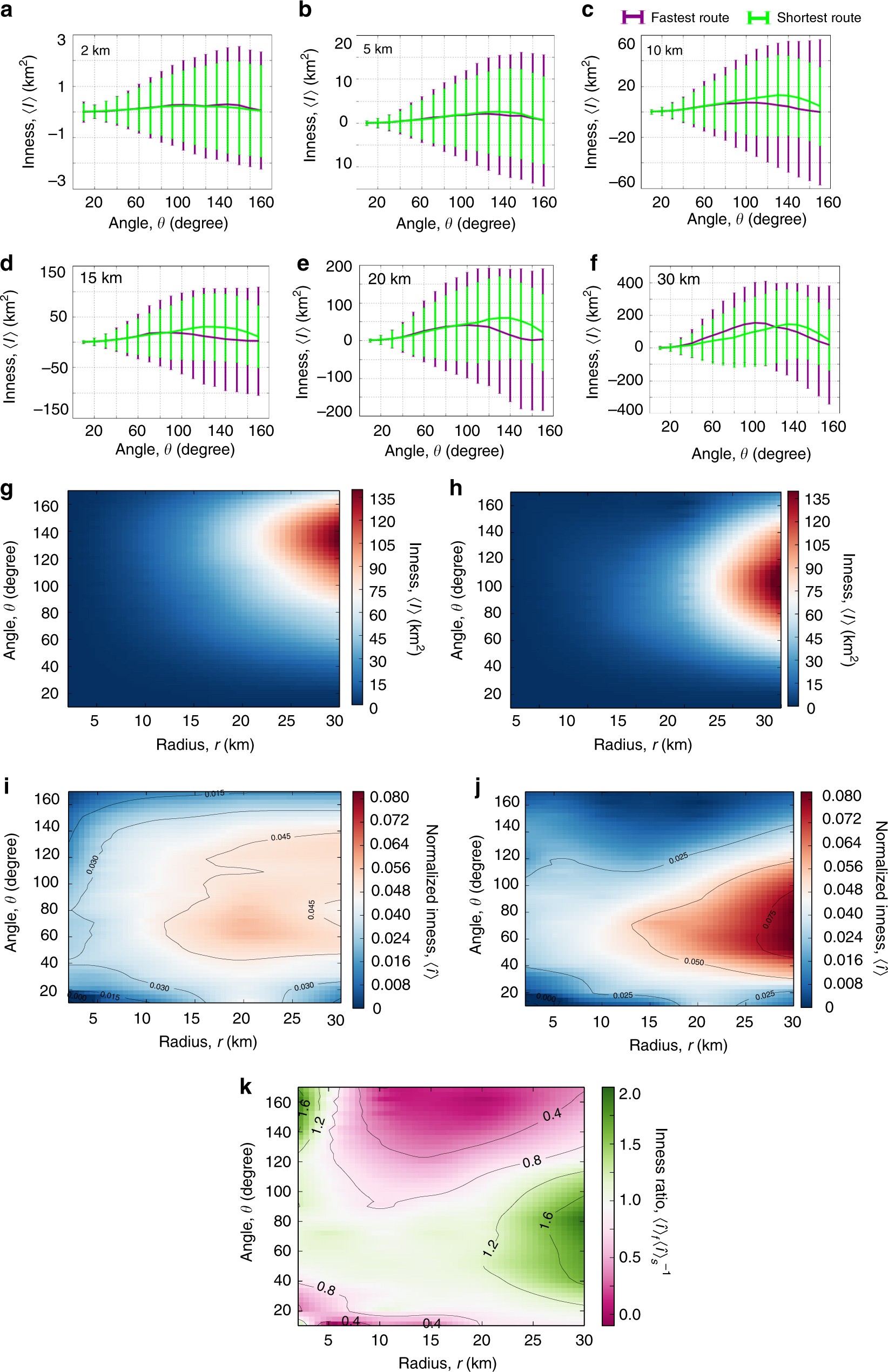
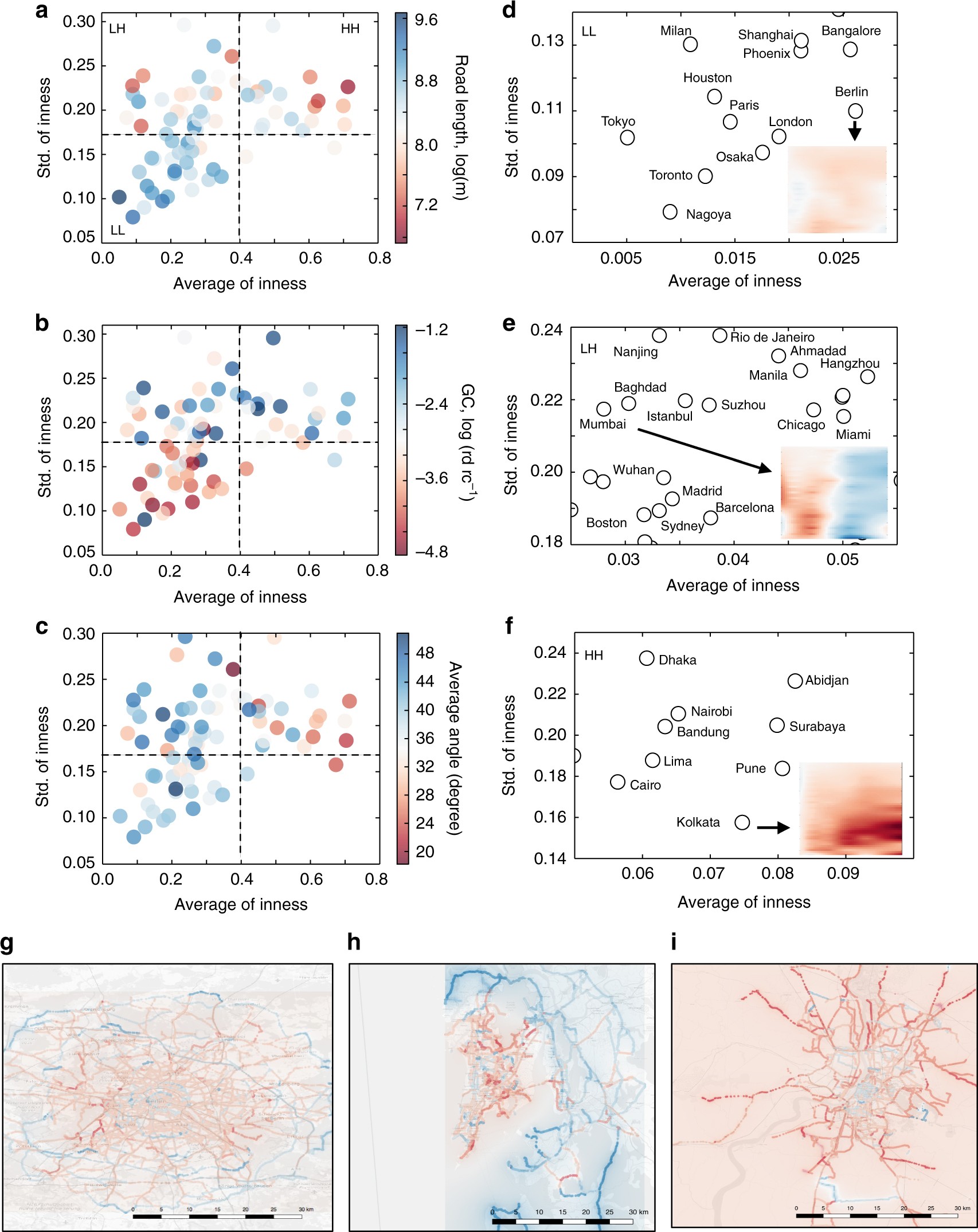
图 个体城市内部分布的统计和空间分布

以每个城市的平均内在度为函数绘制的标准差。城市按其平均值和内部标准差分为三组：低-低（LL）、低-高（LH）、高（HH）。这些点的颜色表示道路长度a、地理约束水平（GC）b，以及外围连通性的度量c。我们扩大了三个标记为LL、LH和HH的区域，并在d-f中明确标注城市，并在插图^I中显示，针对每个地区的代表性城市（柏林、孟买、加尔各答）。在g、h和i中，我们绘制了三个代表性城市的物理地图的空间分布。街道交叉口的颜色对应于所有通过该交叉口的路线的平均^I，其值间隔为0：3^I0：3，随着^I的增加，范围从蓝色到红色

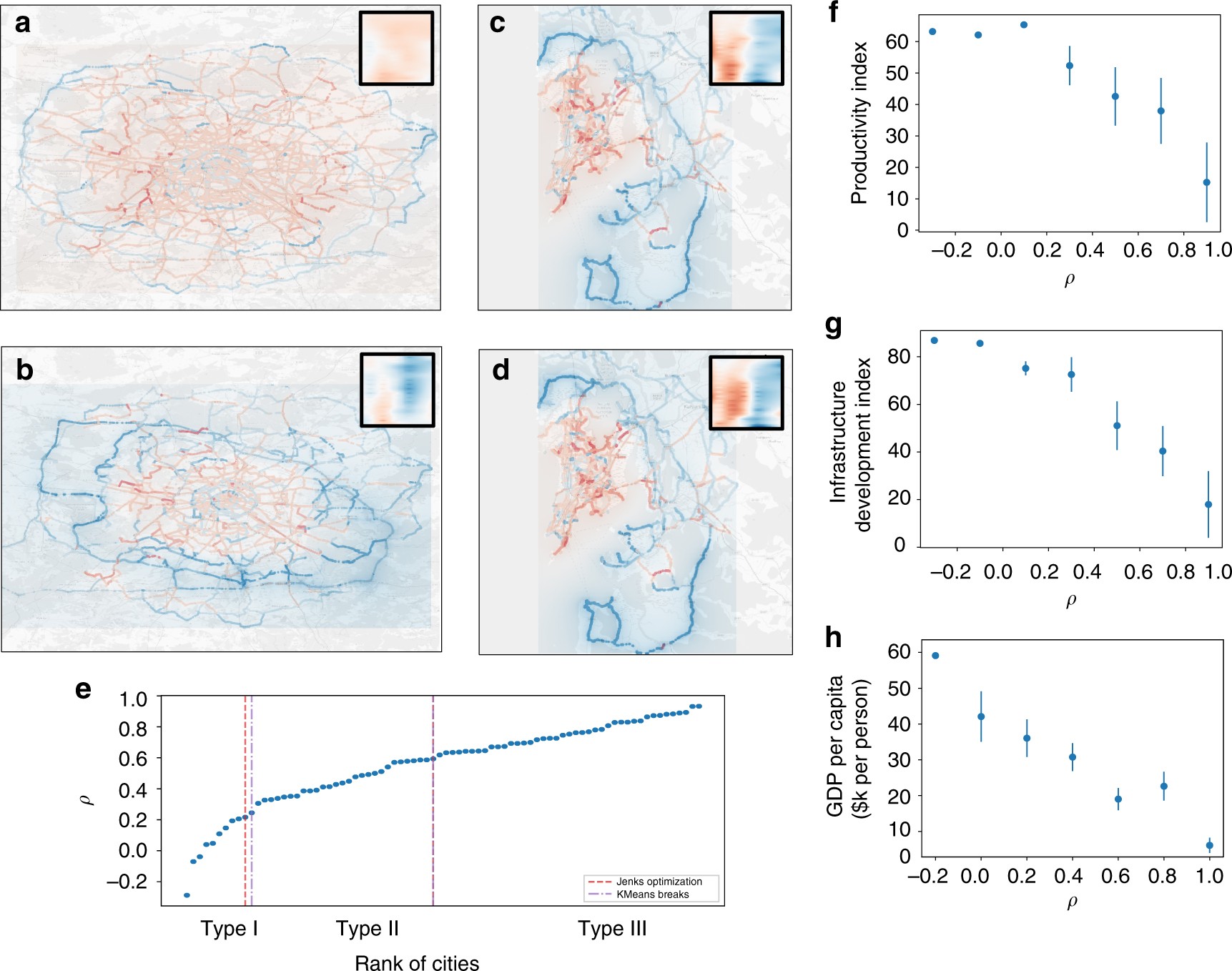
图 最短路线和最快路线之间的区别

最短的路线a和最快的路线b。最短的路线c和到孟买最快的路线d。插图显示了^I的密度图，其范围与图4相同。e每个城市最短和最快路线的内在模式之间的皮尔逊相关系数ρ。根据K-means聚类和Jenks自然断裂优化的相关性水平，将城市分为三组（以垂直虚线标记）。每种类型的城市名称列于补充注6。三个社会经济指数，生产力指数f、基础设施发展指数g和人均GDPh，作为ρ的函数，呈现出明显的单调下降趋势。点是以0.2为间隔进行分类的城市的平均值，条形图表示标准误差

原文链接：https://www.nature.com/articles/s41467-017-02374-7