文章信息：Wei Pan, Gourab Ghoshal, Coco Krumme, Manuel Cebrian & Alex Pentland. (2013). Urban characteristics attributable to density-driven tie formation. Nature Communications: 4, 1961. https://doi.org/10.1038/ncomms2961.

阅读人：刘钊, 2020级博士生

阅读时间：2023年4月2日

选题视角：

从全球来看，目前很大比例的人群生活在人口稠密的城市中心地区，且人口密度呈上升趋势。一个悖论是，尽管大城市存在明显的不利因素，其中包括高犯罪率、交通拥挤、污染或疾病等，但城市地区的密度还在继续提高，更多的人群继续在涌入中心地区。但科学家对于为何大量人口会涌入城市和城市的中心地区，以及大量人口也许可能具有优势的方式却仍不太清楚。

城市化背后的力量非常复杂，因此城市密度增加的背后必然有十分重要的理由和动机。Alex Pentland及其合作者在2013年的Nature Communications刊物上了发表了基于个体之间的社会关系如何形成的一个模型，Urban characteristics attributable to density-driven tie formation。该模型甚至适用于人口非常密集的城市地区。通过复杂网络的相互作用形态，该模型主要考虑的因素包括地理位置、人口密度和个体相互关系。该工作也试图用该模型来解释已知的经验数据，并能得到与实际数据很相似的结果。

基于该模型，他们提供了这样的证据：人口密度和接近度的增加导致社会关系数量的加速增长。进一步而言，城市中人口稠密地区导致更大的社会关系密度，这有助于个体之间的信息流动。该研究表明，这可促进思想交流，进而导致这些地区生产力和创新水平提升。作者进而提出，城市生产力与信息可以传播的距离和速度相关，而城市中心地区特有的高密度社会关系会推动信息的这种流动。

研究背景：

基于地理、人口密度和社会互动之间相互作用的经验证据，我们提出了城市社会结构演变的生成过程。我们的分析和模拟结果预测了社会关系密度的超线性缩放和信息传染作为人口的函数。在这里，我们证明了我们的模型为城市特征与城市规模的依赖关系提供了一个稳健而准确的拟合，从个人层面的二元互动(熟人数量、交流量)到人口层面的变量(传染病率、专利活动、经济生产力和犯罪)，而不需要借助异质性、模块化、专业化或层次结构。

研究梗概：

居住在城市的人口比例比人类历史上任何时期都要大，而城市地区的密度普遍在增加。城市经济学中一个经久不衰的悖论是，尽管犯罪率、污染、疾病和工资溢价不断上升，但与租金溢价相比，人们为什么还在继续向城市迁移?据托马斯·杰斐逊(Thomas Jefferson)所说，18世纪的纽约是“人性所有堕落的厕所”。自杰斐逊时代以来，这座城市已经发展到容纳了100多倍的堕落人口，但新来者的涌入并没有停止。

尽管任何城市移民背后的力量是复杂的，但城市密度带来的优势是一个重要的驱动因素。史密斯4是第一个指出城市中心是创新或堕落的杰出聚集者的人之一。城市似乎支持农村不可能实现的企业水平，城市地区更有效地利用资源，与农村地区相比，人均道路和服务更少，却能产生更多的专利和发明5,6,7,8,9,10。

尽管在科学界和大众中，人们普遍认为密度是城市独特性的驱动因素，但我们仍然缺乏一个令人信服的生成模型，来解释为什么人口聚集可能会带来优势。在几个方面的重要进展凸显了在密度描述水平之外获得对城市过程的理解的困难。早期的集聚经济模型指出了技术扩散在创造智力资本方面的作用，但缺乏对这种扩散如何发生的生成机制的定量描述。层次结构也被认为是这种增长的一种优雅机制14;然而，最近的研究暗示，在地理尺度上缺乏明确的层次结构15,16,17,18,19。人们还观察到，20居民之间的多样性和他们的融合与城市的成功表现出弱相关性，因此促使作者得出结论:“需要更多关于不同学科(或文化、法律和城市特点)的人之间互动的精细数据，才能更好地评估城市创新的不足或过剩表现”。

社交网络研究的最新进展为这一挑战提供了一些线索。经验证据表明，社交网络上的互动和信息交换往往是创意创造、生产力和个人繁荣的驱动力。这方面的例子包括弱关系理论21,22、结构漏洞23、社会互动对经济和社会成功的强作用24、面对面互动对生产力效果的影响，以及信息流在研发管理中的重要性25,26。因此，理解城市中关系形成的机制似乎是发展由经济指标和人口描述的城市增长的一般理论的关键。沿着这条思路，我们提出的城市超线性增长的答案可以被视为克鲁格曼对工业见解的自然延伸6。克鲁格曼指出，制造效率和货物运输之间的关系是工厂邻近度的函数。同样，我们的理论将创意创造和信息流的效率与产生它们的个人的接近度联系起来。

这些思想在城市社会学、城市地理学和经济地理学中有着悠久的渊源。例如，路易斯·沃斯(Louis Wirth)在20世纪30年代末将这些过程概念化(参考文献27)，促使了大量经济地理学文献的出现，这些文献探讨了密度与创新之间的关系，以及扩散(通过社会纽带)与人口密度之间的关系(追溯到20世纪50年代的哈格斯特兰德(参考文献28、29);以及更近一些，但已经确立的关于密度和创造力的文献(例如，参见理查德·佛罗里达的著作30,31,32)。

在本文中，我们提出了一个简单的、自下而上的、完整的模型，描述了城市活力的高效创造和生产力的提高。这篇文章的目标是将这些观点整合到一个单一的数学模型中，从而可以根据现有的经验数据进行测试。我们的模型包含两个基本特征。我们提出了一个简单的分析模型，用于描述个体之间形成的社会关系T(ρ)的数量，并将人口密度ρ作为其单一参数。我们证明，城市人口密度的增加和亲近性导致城市人口社会联系密度的超线性增长。然后，我们表明，沿着这些关系的扩散率——信息流动和思想采纳的数量和速度的代理——准确地再现了城市特征的经验测量规模，如艾滋病/艾滋病毒(获得性免疫缺陷综合症/人类免疫缺陷病毒)感染率、通信和GDP(国内生产总值)。该模型自然会导致指标与城市人口的超线性缩放，而不需要诉诸任何参数调优(尽管它预测的函数形式与简单的幂律不同，与数据的匹配更准确)。在许多不同的城市指标(见补充注1和补充表S1)中惊人地相似的缩放指数，表明它们背后存在共同的机制。因此，社会联系密度和信息流在人类交流模式、人口流动模式和城市经济特征之间提供了一种简约的、可生成的联系，而不需要诉诸等级制度、专业化或类似的社会结构。

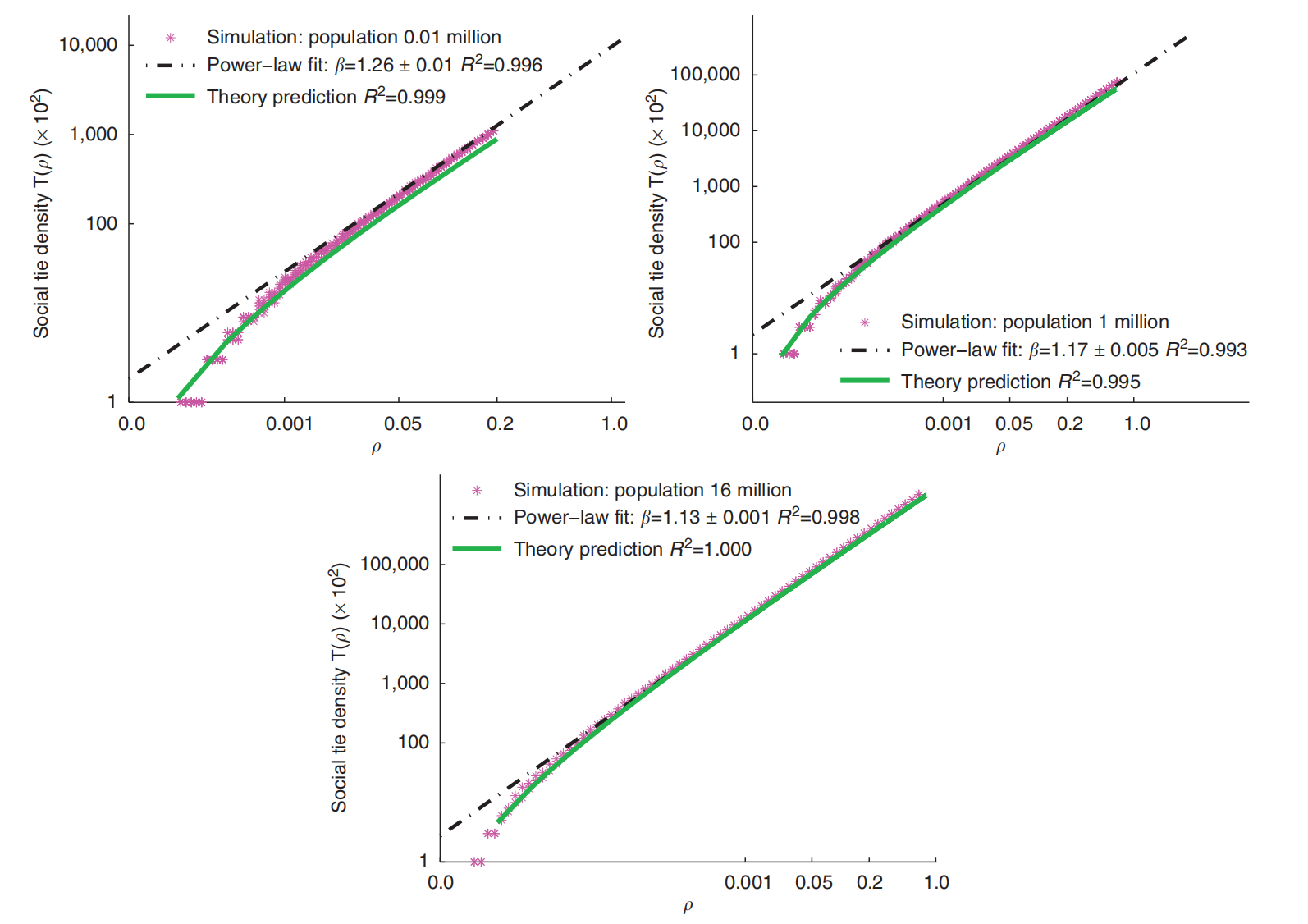
图 社会联系的数量作为网格大小和城市流动性限制的函数

联系的数量T(ρ)绘制为不同网格大小n的ρ的函数。数据点表示文本中描述的模拟的平均超过n=30个实现，而实线绿色是理论表达式方程(5)。虚线是适合的形式。可以看出，在每一种情况下，理论和模拟之间的一致性是极好的。与标度指数的最佳拟合值为β≈1.15，与n无关。值得注意的是，该指数在经验数据中的实测值为1.1≤β≤1.3。

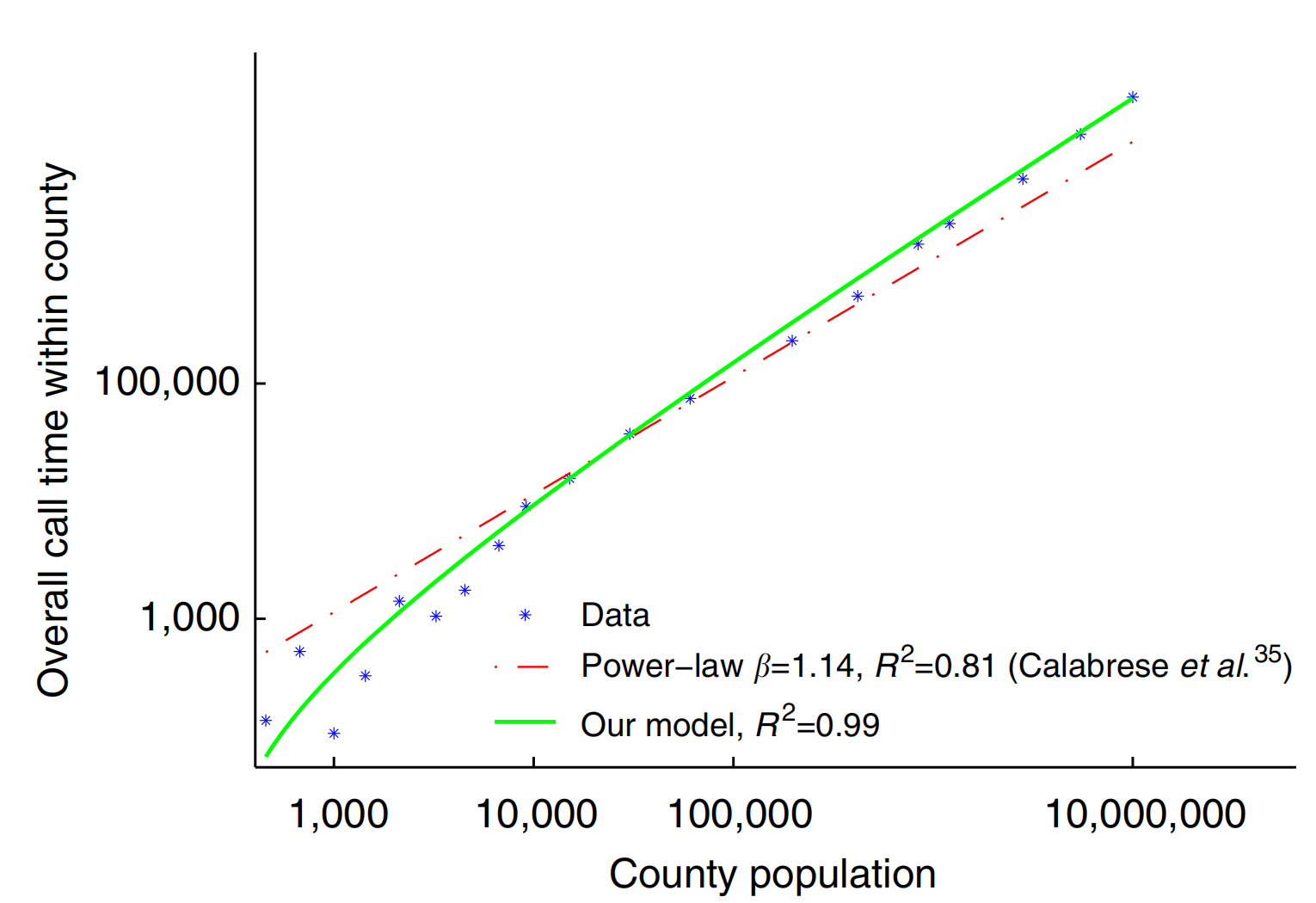
图 一个县的居民之间的总通话时间是其人口的函数

其中点为数据(改编自Calabrese et al.35，根据2010年7月美国境内1000万用户的移动电话通话记录计算)，实线为模型方程(5)适配原始人口的理论预测。该模型捕获了曲线两端的超线性增长和倾斜，同时与纯幂律关系(虚线曲线)相比，提供了更好的数据拟合(基于调整后的r2值)。

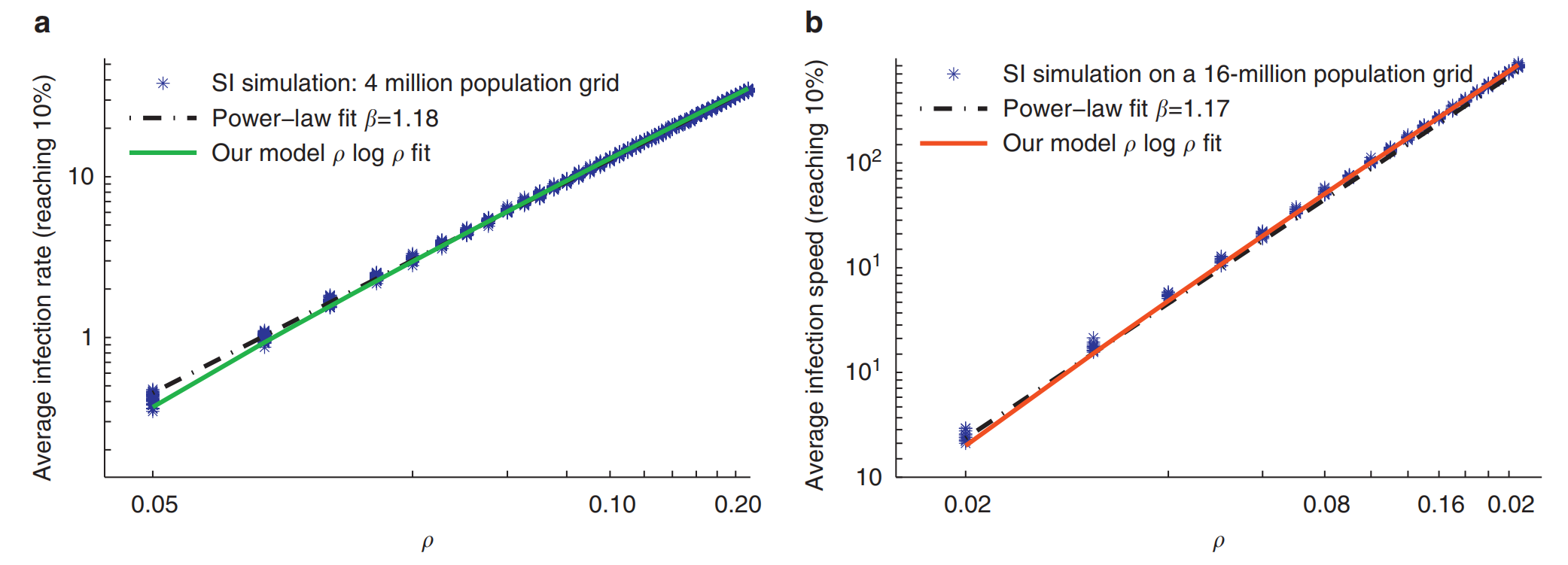
图 对于两种不同的传染模型，传播率作为密度的函数

(a)平均扩散率作为密度ρ的函数。这些点对应于在200 × 200网格上对SI模型进行模拟的n=30个实现。虚线对应于α=0.18的形式拟合。实线符合社会关系密度模型。(b)基于n=30次模拟实现的复杂传染扩散模型下的平均传播率作为ρ的函数。虚线对应于形式的幂律拟合α=0.17。同样，实线是对本文所描述的模型的拟合。在这两种情况下，社会关系密度模型提供了比简单幂律更好的拟合，均方误差要低得多(分别低29%和41%)。

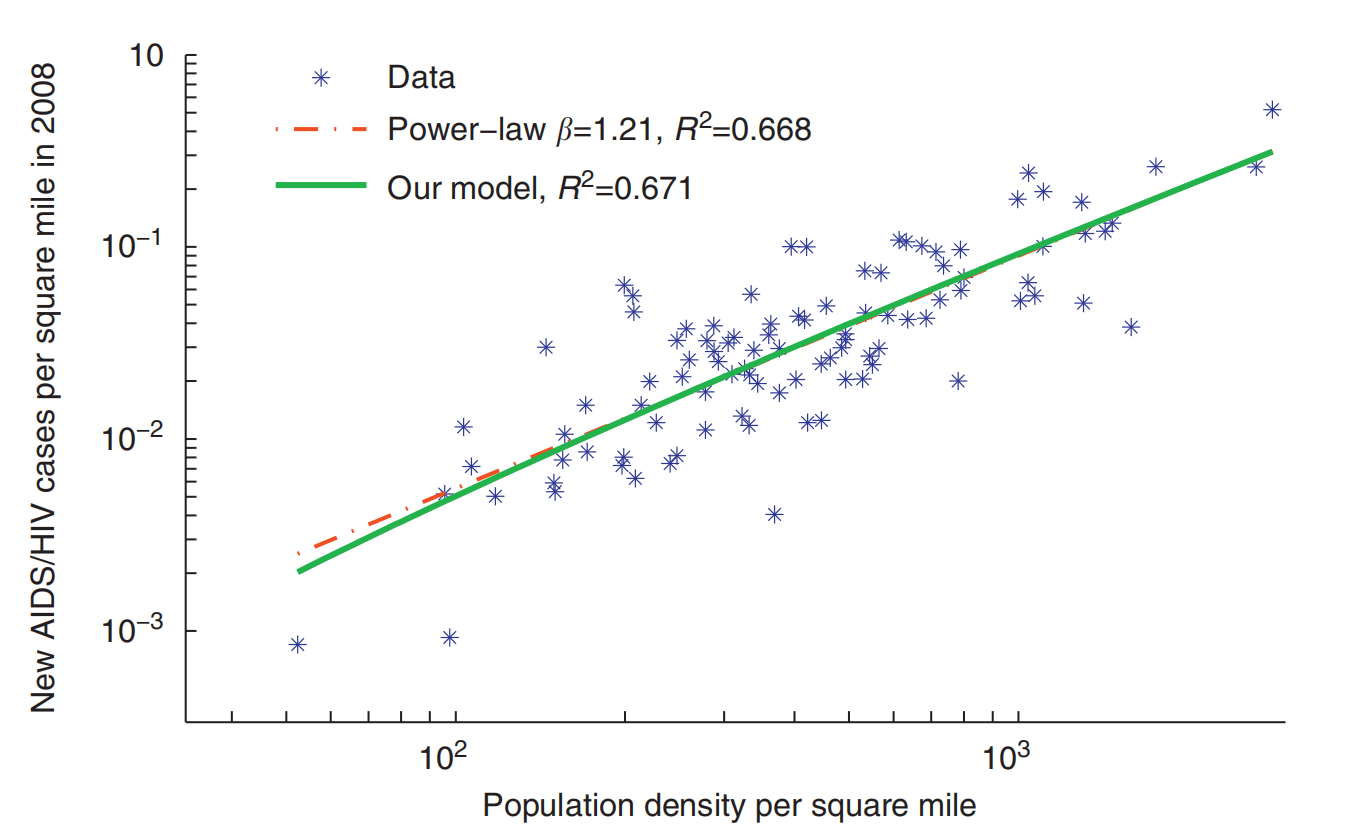
图 美国大都市统计区HIV传播率与密度的函数关系。

最近疾病控制和预防中心和美国人口普查调查的90个大都市统计区域的密度和艾滋病/艾滋病毒传播率之间的关系。可以看到，该模型捕获了数据中的定性趋势。

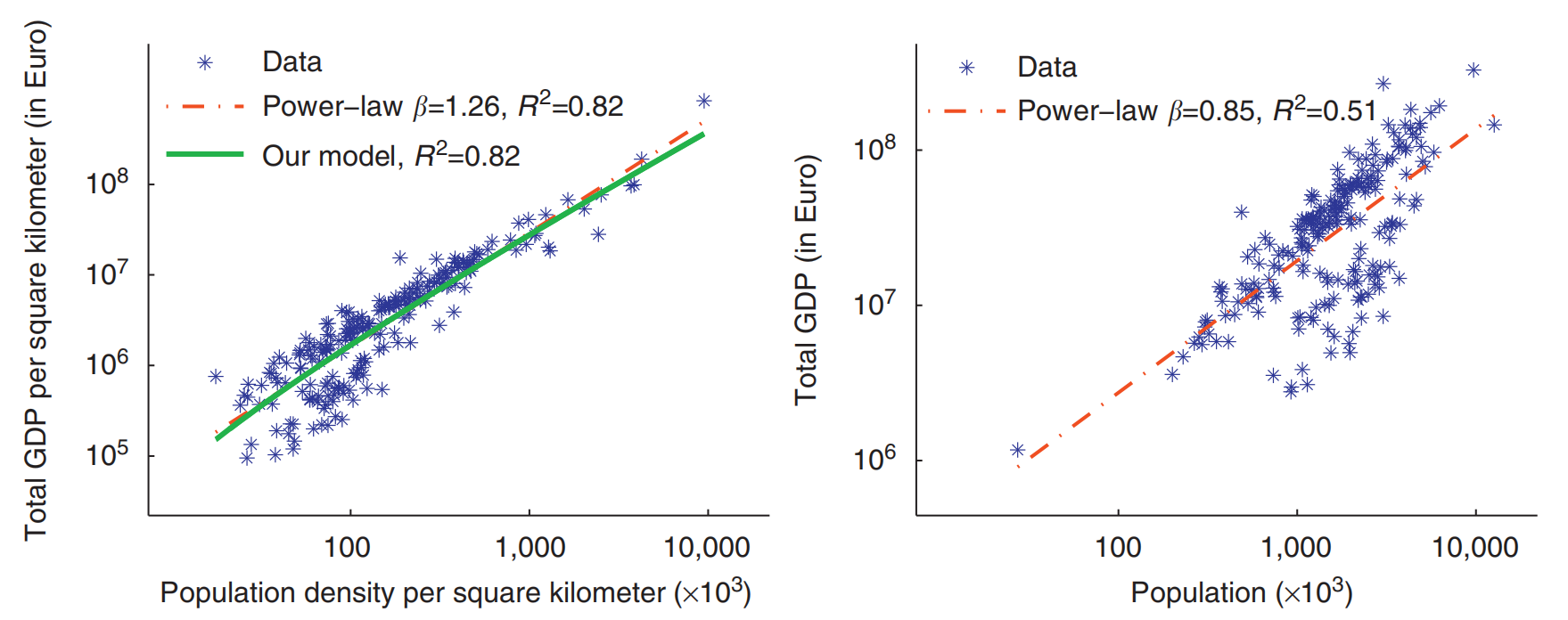
图 欧盟所有247个NUST-2区域的GDP与人口之间的相关性，以及GDP与人口密度之间的相关性

左:密度与GDP之间的相关性，表明与模型预测的超线性泛函形式具有很强的相关性。为了说明性的目的，还显示了适合数据的纯幂律。

右:人口与GDP的相关性，这次呈现次线性函数形式。然而，较低的r2值表明，原始人口和城市密度与GDP增长并不相关。

原文链接：https://www.nature.com/articles/ncomms2961