文章信息：Meead Saberi, Homayoun Hamedmoghadam, Mudabber Ashfaq, Seyed Amir Hosseini, Ziyuan Gu, Sajjad Shafiei, Divya J. Nair, Vinayak Dixit, Lauren Gardner, S. Travis Waller, & Marta C. González. (2020). A simple contagion process describes spreading of traffic jams in urban networks. Nature Communications: 11(1), 1616. https://doi.org/10.1038/s41467-020-15353-2  

阅读笔记：王舜奕

阅读时间：2020年11月26日

文章摘要：

Abstract: The spread of traffic jams in urban networks has long been viewed as a complex spatiotemporal phenomenon that often requires computationally intensive microscopic models for analysis purposes. In this study, we present a framework to describe the dynamics of congestion propagation and dissipation of traffic in cities using a simple contagion process, inspired by those used to model infectious disease spread in a population. We introduce two macroscopic characteristics for network traffic dynamics, namely congestion propagation rateβand congestion dissipation rateμ. We describe the dynamics of congestion spread using these new parameters embedded within a system of ordinary differential equations, similar to the well-known susceptible-infected-recovered (SIR) model. The proposed contagion-based dynamics are verified through an empirical multi-city analysis, and can be used to monitor, predict and control the fraction of congested links in the network over time.

摘要：交通堵塞在城市网络中的蔓延长期以来被视为一种复杂的时空现象，通常需要密集计算的微观模型来进行分析。在本研究中，我们提出了一个框架使用一个简单的传染过程来描述拥挤传播和交通耗散的动力学，灵感来自于那些用于传染病在人口中传播的模型。我们引入了网络流量动态的两个宏观特征，即拥塞传播率极小值和拥塞耗散率极小值。我们使用嵌入在常微分方程系统中的这些新参数来描述拥塞扩散的动力学，类似于著名的易感染-感染-恢复(SIR)模型。提出的基于传染的动态通过经验的多城市分析得到验证，并可用于监测、预测和控制网络中拥堵路段的比例随着时间的推移。

选题视角

城市里的交通拥堵，会随着时间和空间蔓延。现有的城市交通建模方法往往依赖于微观模型，计算量大，校准需要过多的参数化。

许多研究探索了不同的宏观方法来模拟城市交通拥堵的蔓延，包括通过渗透理论，机器学习方法，和排队理论，这些模型无法捕捉和定量描述拥塞在时间和空间中的传播和消散模式。

交通系统显示潜在的传播动力学类似于那些观察和应用于其他网络系统，例如，社会网络，人口联系网络，或技术网络，特别是描述传染病在人群中传播的网络。

主要结论

基于传播和耗散的交通堵塞在城市可以被描述为一个简单的蔓延过程,拥塞传播确实是一种传播现象，类似于著名的SIR（susceptible-infected-recovered）模型。

依赖于两个宏观网络交通流特征,即拥堵传播和拥堵恢复。网络中拥塞增加的程度以及恢复的速度取决于传播率与恢复率的比率，该比率由基本再生数R0表示。

时间依赖的出行需求曲线，对网络中拥塞传播和消散的动态产生影响，对于任何给定的交通需求增加，R0都会增加，交通堵塞的规模将变得更大，需要更长的时间来恢复对旅行需求的响应。

通过对6个不同城市的实证数据进行分析，验证了提出的传染模型的有效性，在宏观水平上，它们往往具有一致的拥塞传播动态。

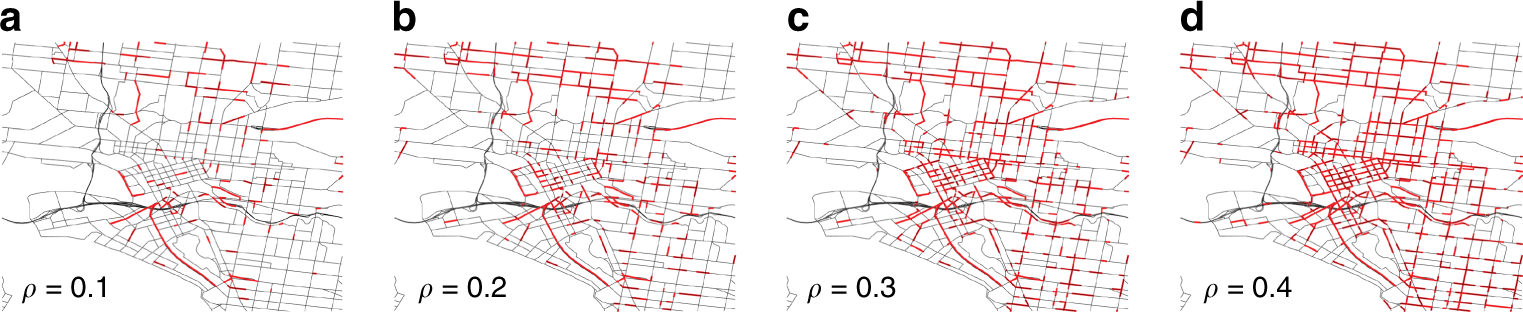
图 墨尔本网络拥堵的空间分布。在给定时间t=8:30上午，地图显示了当aρ=0.1、bρ=0.2、cρ=0.3和dρ=0.4时网络上的拥堵路段（编码为红色）。

图 描述拥塞的时间演化。网络中拥塞传播的两态模型:一部分拥塞链路c(t)与时间的关系，导致由一个变化的SI模型描述的完全网络堵塞和b部分网络堵塞由一个变化的SIS模型描述。网络中拥塞传播和消散的三维模型，类似于受时变装卸需求剖面影响的SIR模型。

图 六个不同城市的拥堵传播和消散动力学经验证据。R0与rep的关系。对于较小的价值，尽管不同城市在网络结构、需求和交通模式上存在差异，但在观察到的动态中存在一致性。对于较小的c值，对于相同的c值，R0大致保持不变，这表明存在一种用于拥塞传播的通用措施;b每个城市在早上6点至10点期间网络拥塞链路的比例（t） ，当前城市保持率=0.2时。拥塞开始和偏移用虚线标记。注意，y轴有一个固定的范围[0,0.035]，并且利用拥塞开始和偏移时间之间的数据子集来拟合SIR模型；c网络恢复链路比例r（t）随时间的演化;网络中自由流连接的比例f（t）随时间的演化。

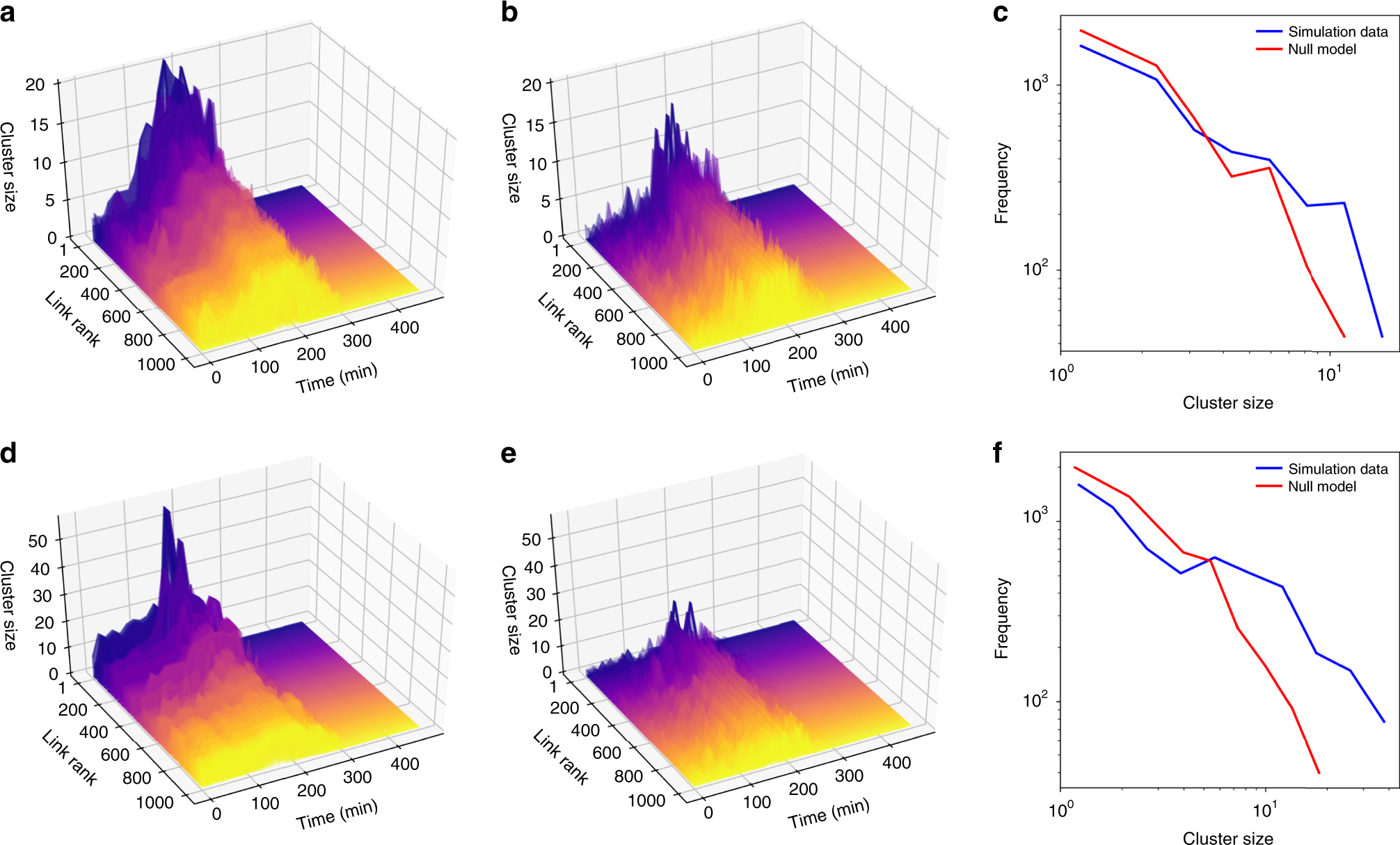
图 与拥塞链路相关的上游簇的进化情况。这里,a和d显示随时间变化在拥挤的集群的大小与链接在墨尔本交通网络,而b和e描述相同的结果为零模型生成独立对每个时间步通过随机λi(t)为每个链接i来自同一分布的模拟数据;链接按照其拥挤的上游集群的最大大小进行排序，结果只显示前1000个链接。比较了在t = 180时，ρ= 0.5和ρ=0.7时，墨尔本交通仿真模型和null模型对应的拥堵上游集群的规模分布情况。与链路相对速度分布相同、结构相同的空模型相比，墨尔本交通网络模型中上游集群更频繁地出现较大的拥塞现象。

原文链接：https://www.nature.com/articles/s41467-020-15353-2