文章信息：Marta C. González, César A. Hidalgo, & Albert-László Barabási. (2008). Understanding individual human mobility patterns. Nature: 453(7196), 779–782. https://doi.org/10.1038/nature06958

推荐人：王舜奕

整理人：杨文，2023级硕士生

整理时间：2024年8月25日

Abstract: Despite their importance for urban planning1, traffic forecasting2 and the spread of biological3,4,5 and mobile viruses6, our understanding of the basic laws governing human motion remains limited owing to the lack of tools to monitor the time-resolved location of individuals. Here we study the trajectory of 100,000 anonymized mobile phone users whose position is tracked for a six-month period. We find that, in contrast with the random trajectories predicted by the prevailing Lévy flight and random walk models7, human trajectories show a high degree of temporal and spatial regularity, each individual being characterized by a time-independent characteristic travel distance and a significant probability to return to a few highly frequented locations. After correcting for differences in travel distances and the inherent anisotropy of each trajectory, the individual travel patterns collapse into a single spatial probability distribution, indicating that, despite the diversity of their travel history, humans follow simple reproducible patterns. This inherent similarity in travel patterns could impact all phenomena driven by human mobility, from epidemic prevention to emergency response, urban planning and agent-based modelling.

摘要：尽管它们对城市规划1、交通预测2以及生物3、4、5和移动病毒6的传播具有重要意义，但由于缺乏监测个体时间分辨位置的工具，我们对人类运动基本规律的理解仍然有限。在这里，我们研究了10万名匿名手机用户的轨迹，他们的位置被跟踪了六个月。我们发现，与流行的莱维飞行和随机行走模型7预测的随机轨迹相比，人类轨迹表现出高度的时间和空间规律性，每个人的特征是与时间无关的特征旅行距离和返回几个高频率地点的显著概率。在校正了旅行距离的差异和每条轨迹的固有各向异性后，个体的旅行模式崩溃为单一的空间概率分布，这表明，尽管人类的旅行历史存在多样性，但他们遵循简单的可重复模式。旅行模式的这种内在相似性可能会影响由人类流动驱动的所有现象，从流行病预防到应急响应、城市规划和基于代理的建模。

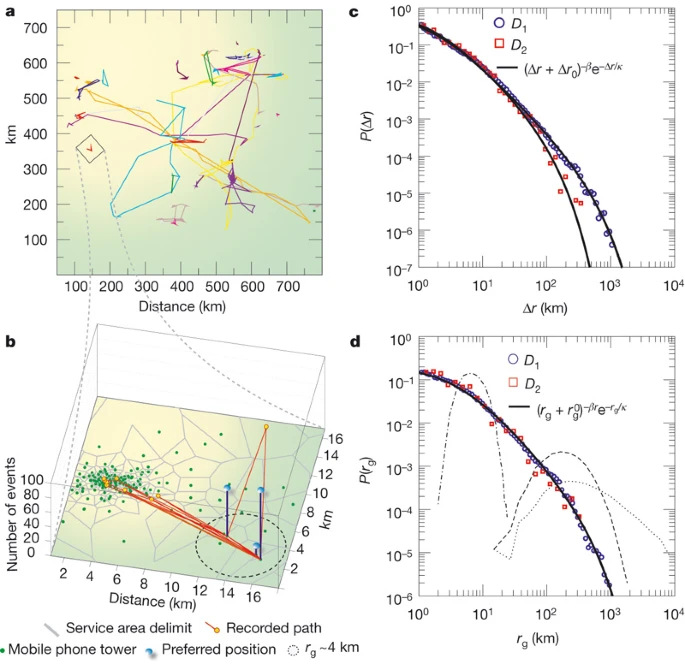
图 基本的人员流动模式

a、 40名手机用户的一周轨迹表明，大多数人只走很短的距离，但也有少数人经常走数百公里。b、 单个用户的详细轨迹。不同的电话塔显示为绿点，灰色的沃罗诺伊格子标记了每个塔的大致接收区域。我们研究的数据集只记录了离移动用户最近的塔的身份；因此，我们无法识别用户在Voronoi小区内的位置。b中所示的用户轨迹是由186个两小时报告构建的，在此期间，用户总共访问了12个不同的位置（塔附近）。其中，用户在两个最受欢迎的位置分别出现了96次和67次；每个位置的访问频率显示为垂直条。圆圈代表以轨迹质心为中心的回转半径。c、 为两个研究数据集D1和D2获得的行进距离的概率密度函数P（Δr）。实线表示截断幂律，其参数在文本中提供（见方程式（1））。d、 为用户测量的回转半径分布P（rg），其中rg（T）是在T=6个月的观察后测量的。实线表示类似的截断幂律拟合（见方程式（2））。虚线、点划线和点划线曲线显示了从标准零模型（分别为RW、LF和TLF）获得的P（rg），其中对于TLF，我们使用了与移动电话用户测量的步长分布相同的步长分布。

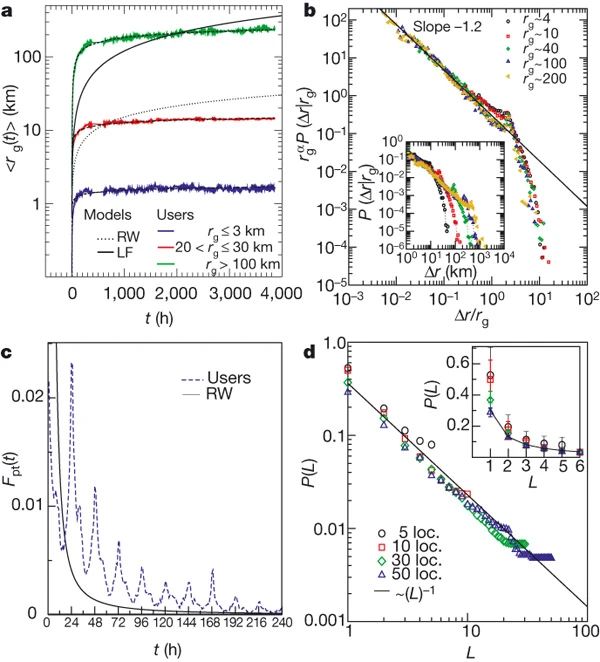
图 人类轨迹的有限性

a、 根据最终rg（t）分为三组的手机用户的回转半径〈rg（t）〉与时间的关系，其中t=6个月。黑色曲线与随机游走模型的分析预测相对应，随时间增加为〈rg（t）〉|LF、TLF∼t3/2+β（实线）和〈rg（t）〉|RW∤t0.5（虚线）。对应于a+B ln（t）形式的对数拟合的虚线曲线，其中a和B是与时间无关的系数，取决于rg.B，rg=4、10、40、100和200公里的用户的个体行驶距离P（Δr|rg）的概率密度函数。如插图所示，每组显示了完全不同的P（Δr |rg）分布。在用rg（主面板）重新缩放距离和分布后，不同的曲线会崩溃。实线（幂律）显示为眼睛的向导。c、 返回概率分布，Fpt（t）。与随机行走预测的平滑渐近行为∼1/（t ln（t）2）（实线）相反，突出的峰值捕捉到了人类定期返回他们之前访问过的位置的趋势。d、 Zipf图显示了访问不同地点的频率（位置）。这些符号对应于被观察到访问nL=5、10、30和50个不同位置的用户。用（L）表示访问频率顺序中列出的位置的排名，数据很好地近似为R（L）∠L-1。插图是线性比例的相同图，说明40%的时间个体出现在它们的前两个首选位置；条形图表示标准误差。

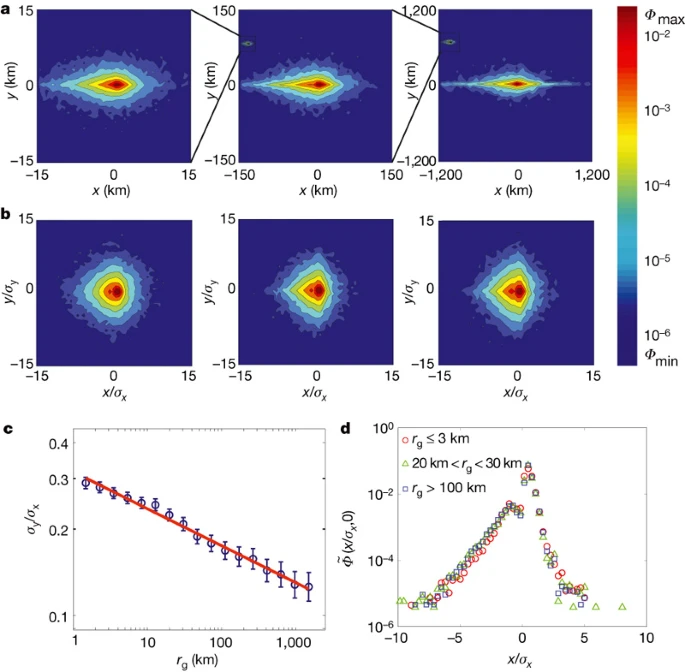
图 人类轨迹的形状

a、 在用户固有参考系中的位置（x，y）找到移动电话用户的概率密度函数Φ（x，y）（详见补充信息）。从左到右的三个图是为10000名用户生成的：rg≤3，20<rg≤30和rg>100km。随着rg的增加，轨迹变得更加各向异性。b、 在用σx和σy缩放每个位置后，每个组的结果形状大致相同。c、 Φ（x，y）形状的变化可以量化，计算各向同性比S≡σy/σx作为rg的函数，它随着（实线）的减小而减小。误差条表示标准误差。d、 表示b中所示的重新缩放分布的x轴横截面。

原文链接：https://www.nature.com/articles/nature06958#Fig2